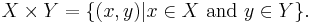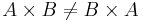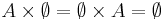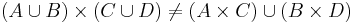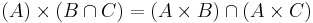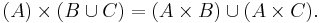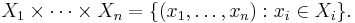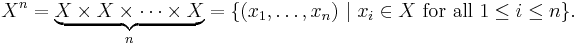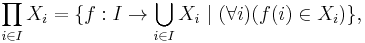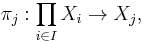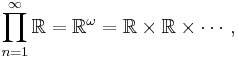Cartesian product

In mathematics, a Cartesian product (or product set) is the direct product of two sets. The Cartesian product is named after René Descartes,^[1] whose formulation of analytic geometry gave rise to this concept.

Specifically, the Cartesian product of two sets X (for example the points on an x-axis) and Y (for example the points on a y-axis), denoted X × Y, is the set of all possible ordered pairs whose first component is a member of X and whose second component is a member of Y (e.g., the whole of the x–y plane):

$X\times Y = \{(x,y) | x\in X \ \text{and} \ y\in Y\}.$ ^[2]

For example, the Cartesian product of the 13-element set of standard playing card ranks {Ace, King, Queen, Jack, 10, 9, 8, 7, 6, 5, 4, 3, 2} and the four-element set of card suits {♠, ♥, ♦, ♣} is the 52-element set of all possible playing cards: ranks × suits = {(Ace, ♠), (King, ♠), ..., (2, ♠), (Ace, ♥), ..., (3, ♣), (2, ♣)}. The corresponding Cartesian product has 52 = 13 × 4 elements. The Cartesian product of the suits × ranks would still be the 52 pairings, but in the opposite order {(♠, Ace), (♠, King), ...}. Ordered pairs (a kind of tuple) have order, but sets are unordered. The order in which the elements of a set are listed is irrelevant; you can shuffle the deck and it's still the same set of cards.

A Cartesian product of two finite sets can be represented by a table, with one set as the rows and the other as the columns, and forming the ordered pairs, the cells of the table, by choosing the element of the set from the row and the column.

1 Basic properties
2 n-ary product
3 Cartesian square and Cartesian power
4 Infinite products
5 Abbreviated form
6 Cartesian product of functions
7 Category theory
8 Graph theory
9 See also
10 Notes
11 External links

Basic properties

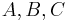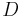Let $A, B, C$ , and $D$ be sets.

In cases where the two input sets are not the same, the Cartesian product is not commutative because the ordered pairs are reversed.

Although the elements of each of the ordered pairs in the sets will be the same, the pairing will differ.

$A \times B \neq B \times A$

For example:

{1,2} x {3,4} = {(1,3), (1,4), (2,3), (2,4)}

{3,4} x {1,2} = {(3,1), (3,2), (4,1), (4,2)}

One exception is with the empty set, which acts as a "zero", and for equal sets.

$A \times \emptyset = \emptyset \times A = \emptyset$

and, supposing G,T are sets and G=T:

$(G) \times (T) = (T) \times (G).$

Strictly speaking, the Cartesian Product is not associative.

$(A\times B)\times C \neq A \times (B \times C)$

The Cartesian Product acts nicely with respect to intersections.

$(A \cap B) \times (C \cap D) = (A \times C) \cap (B \times D)$

Notice that in most cases the above statement is not true if we replace intersection with union.

$(A \cup B) \times (C \cup D) \neq (A \times C) \cup (B \times D)$

However, for intersection and union it holds for:

$(A) \times (B \cap C) = (A \times B) \cap (A \times C)$

and,

$(A) \times (B \cup C) = (A \times B) \cup (A \times C).$

`n`-ary product

The Cartesian product can be generalized to the n-ary Cartesian product over n sets X₁, ..., X_n:

$X_1\times\cdots\times X_n = \{(x_1, \ldots, x_n)�: x_i \in X_i \}.$

It is a set of n-tuples. If tuples are defined as nested ordered pairs, it can be identified to (X₁ × ... × X_n-1) × X_n.

Cartesian square and Cartesian power

The Cartesian square (or binary Cartesian product) of a set X is the Cartesian product X² = X × X. An example is the 2-dimensional plane R² = R × R where R is the set of real numbers - all points (x,y) where x and y are real numbers (see the Cartesian coordinate system).

The cartesian power of a set X can be defined as:

$X^n = \underbrace{ X \times X \times \cdots \times X }_{n}= \{ (x_1,\ldots,x_n) \ | \ x_i \in X \ \text{for all} \ 1 \le i \le n \}.$

An example of this is R³ = R × R × R, with R again the set of real numbers, and more generally Rⁿ.

The n-ary cartesian power of a set X is isomorphic to the space of functions from an n-element set to X. As a special case, the 0-ary cartesian power of X may be taken to be a singleton set, corresponding to the empty function with codomain X.

Infinite products

It is possible to define the Cartesian product of an arbitrary (possibly infinite) family of sets. If I is any index set, and {X_i | i ∈ I} is a collection of sets indexed by I, then the Cartesian product of the sets in X is defined to be

$\prod_{i \in I} X_i = \{ f�: I \to \bigcup_{i \in I} X_i\ |\ (\forall i)(f(i) \in X_i)\},$

that is, the set of all functions defined on the index set such that the value of the function at a particular index i is an element of X_i .

For each j in I, the function

$\pi_{j}�: \prod_{i \in I} X_i \to X_{j},$

defined by π_j(f) = f(j) is called the j -th projection map.

An important case is when the index set is N the natural numbers: this Cartesian product is the set of all infinite sequences with the i -th term in its corresponding set X_i. For example, each element of

$\prod_{n = 1}^\infty \mathbb R =\mathbb{R}^\omega= \mathbb R \times \mathbb R \times \cdots,$

can be visualized as a vector with an infinite number of real-number components.

The special case Cartesian exponentiation occurs when all the factors X_i involved in the product are the same set X. In this case,

$\prod_{i \in I} X_i = \prod_{i \in I} X$

is the set of all functions from I to X. This case is important in the study of cardinal exponentiation.

The definition of finite Cartesian products can be seen as a special case of the definition for infinite products. In this interpretation, an n-tuple can be viewed as a function on {1, 2, ..., n} that takes its value at i to be the i-th element of the tuple (in some settings, this is taken as the very definition of an n-tuple).

Nothing in the definition of an infinite Cartesian product implies that the Cartesian product of nonempty sets must itself be nonempty. This assertion is equivalent to the axiom of choice.

Abbreviated form

If several sets are being multiplied together, e.g. X₁, X₂, X₃, …, then some authors^[3] choose to abbreviate the Cartesian product as simply ×X_i.

Cartesian product of functions

If f is a function from A to B and g is a function from X to Y, their cartesian product f×g is a function from A×X to B×Y with

$(f\times g)(a, b) = (f(a), g(b)).$

As above this can be extended to tuples and infinite collections of functions.

Category theory

Although the Cartesian product is traditionally applied to sets, category theory provides a more general interpretation of the product of mathematical structures. This is distinct from, although related to, the notion of a Cartesian square in category theory, which is a generalization of the fiber product.

Graph theory

In graph theory the Cartesian product of two graphs G and H is the graph denoted by G×H whose vertex set is the (ordinary) Cartesian product V(G)×V(H) and such that two vertices (u,v) and (u′,v′) are adjacent in G×H if and only if u is adjacent to u′ and v is adjacent to v′. Unlike the ordinary Cartesian product, the Cartesian product of graphs is not a product in the sense of category theory. Instead it is more like a tensor product.

Notes

↑ cartesian. (2009). In Merriam-Webster Online Dictionary. Retrieved December 1, 2009, from http://www.merriam-webster.com/dictionary/cartesian
↑ Warner, S: Modern Algebra, page 6. Dover Press, 1990.
↑ Osborne, M., and Rubinstein, A., 1994. A Course in Game Theory. MIT Press.

External links

Cartesian Product at ProvenMath